Merge Sort

Merge Sort follows the rule of Divide and Conquer to sort a given set of numbers/elements, recursively, hence consuming less time.

In the last two tutorials, we learned about Selection Sort and Insertion Sort, both of which have a worst-case running time of O(n²). As the size of input grows, insertion and selection sort can take a long time to run. Merge sort, on the other hand, runs in O(nlog n) time in all the cases.

Before jumping on to, how merge sort works and its implementation, first let’s understand what the rule of Divide and Conquer is?

Divide and Conquer

If we can break a single big problem into smaller sub-problems, solve the smaller sub-problems and combine their solutions to find the solution for the original big problem, it becomes easier to solve the whole problem.

Let's take a historical example of Divide and Rule.

When Britishers came to India, they saw a country with different religions living in harmony, hard working but naive citizens, unity in diversity, and found it difficult to establish their empire. So, they adopted the policy of Divide and Rule. Where the population of India was collectively a one big problem for them, they divided the problem into smaller problems, by instigating rivalries between local kings, making them stand against each other, and this worked very well for them.

Well that was history, and a socio-political policy (Divide and Rule), but the idea here is, if we can somehow divide a problem into smaller sub-problems, it becomes easier to eventually solve the whole problem.

In Merge Sort, the given unsorted array with n elements is divided into n sub-arrays, each having one element, because a single element is always sorted in itself. Then, it repeatedly merges these sub-arrays, to produce new sorted sub-arrays, and in the end, one complete sorted array is produced.

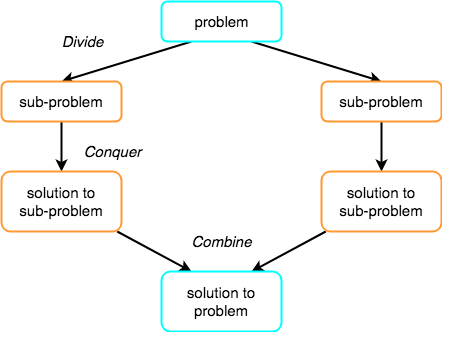
The concept of Divide and Conquer involves three steps:

1. Divide the problem into multiple small problems.
2. Conquer the sub problems by solving them. The idea is to break down the problem into atomic sub problems, where they are actually solved.
3. Combine the solutions of the sub problems to find the solution of the actual problem.

How Merge Sort Works?

As we have already discussed that merge sort utilizes divide-and-conquer rule to break the problem into sub-problems, the problem in this case being, sorting a given array.

In merge sort, we break the given array midway, for example if the original array had 6 elements, then merge sort will break it down into two sub-arrays with 3 elements each. But breaking the original array into 2 smaller sub-arrays is not helping us in sorting the array.

So we will break these sub-arrays into even smaller sub-arrays, until we have multiple sub-arrays with single element in them. Now, the idea here is that an array with a single element is already sorted, so once we break the original array into sub-arrays which has only a single element, we have successfully broken down our problem into base problems. And then we have to merge all these sorted sub-arrays, step by step to form one single sorted array.

Let's consider an array with values {14, 7, 3, 12, 9, 11, 6, 12}

Below, we have a pictorial representation of how merge sort will sort the given array.

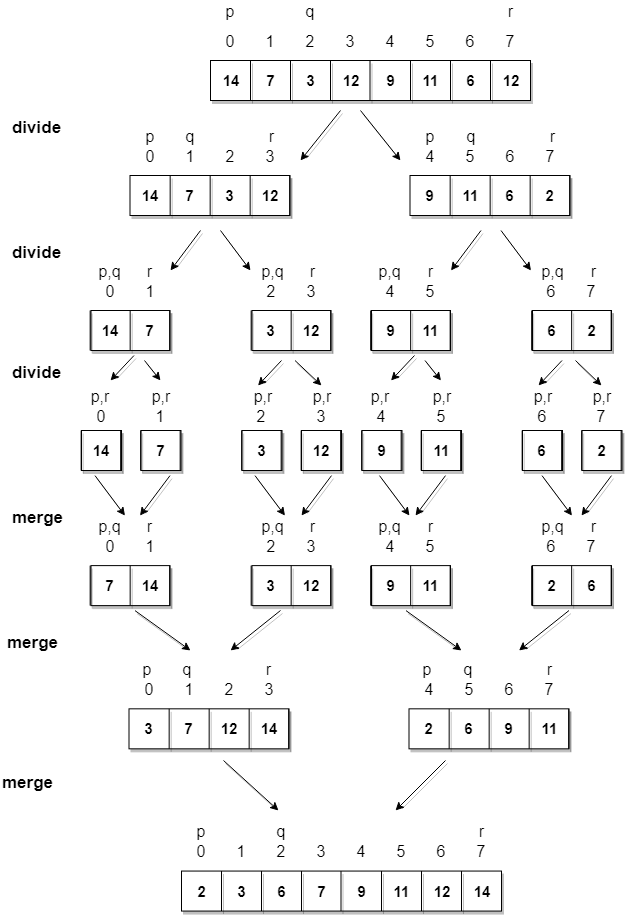
In merge sort we follow the following steps:

1. We take a variable p and store the starting index of our array in this. And we take another variable r and store the last index of array in it.
2. Then we find the middle of the array using the formula (p + r)/2 and mark the middle index as q, and break the array into two sub-arrays, from p to q and from q + 1 to r index.
3. Then we divide these two sub-arrays again, just like we divided our main array and this continues.
4. Once we have divided the main array into sub-arrays with single elements, then we start merging the sub-arrays.

Implementing Merge Sort Algorithm

Merge Sort C Code

#include<stdio.h>

void mergeSort(int[],int,int);
void merge(int[],int,int,int);

void mergeSort(int a[], int p, int r)
{
    int q;
    if(p < r)
    {
        q = (p + r) / 2;
        mergeSort(a, p, q);
        mergeSort(a, q+1, r);
        merge(a, p, q, r);
    }
}

// function to merge the subarrays
void merge(int a[], int p, int q, int r)
{
    int b[5];   //same size of a[]
    int i, j, k;
    k = 0;
    i = p;
    j = q + 1;
    while(i <= q && j <= r)
    {
        if(a[i] < a[j])
        {
            b[k++] = a[i++];    // same as b[k]=a[i]; k++; i++;
        }
        else
        {
            b[k++] = a[j++];
        }
    }
  
    while(i <= q)
    {
        b[k++] = a[i++];
    }
  
    while(j <= r)
    {
        b[k++] = a[j++];
    }
  
    for(i=r; i >= p; i--)
    {
        a[i] = b[--k];  // copying back the sorted list to a[]
    } 
}

// function to print the array
void printArray(int a[], int size)
{
    int i;
    for (i=0; i < size; i++)
    {
        printf("%d ", a[i]);
    }
    printf("\n");
}
 
int main()
{
    int arr[] = {32, 45, 67, 2, 7};
    int len = sizeof(arr)/sizeof(arr[0]);
 
    printf("Given array: \n");
    printArray(arr, len);
    
    // calling merge sort
    mergeSort(arr, 0, len - 1);
 
    printf("\nSorted array: \n");
    printArray(arr, len);
    return 0;
}

Output

Given array:
32 45 67 2 7

Sorted array:
2 7 32 45 67

Complexity Analysis of Merge Sort

Merge Sort is quite fast, and has a time complexity of O(n*log n). It is also a stable sort, which means the "equal" elements are ordered in the same order in the sorted list.

In this section we will understand why the running time for merge sort is O(n*log n).

As we have already learned in Binary Search that whenever we divide a number into half in every step, it can be represented using a logarithmic function, which is log n and the number of steps can be represented by log n + 1(at most).

Also, we perform a single step operation to find out the middle of any sub-array, i.e. O(1). And to merge the sub-arrays, made by dividing the original array of n elements, a running time of O(n) will be required.

Hence the total time for mergeSort function will become n(log n + 1), which gives us a time complexity of O(n*log n).

Summary

• Worst Case Time Complexity [ Big-O ]: O(n*log n)
• Best Case Time Complexity [Big-omega]: Ω(n*log n)
• Average Time Complexity [Big-theta]: Θ(n*log n)
• Space Complexity: O(n)

Note

• Time complexity of Merge Sort is O(n*Log n) in all the 3 cases (worst, average and best) as merge sort always divides the array in two halves and takes linear time to merge two halves.
• It requires equal amount of additional space as the unsorted array. Hence it’s not at all recommended for searching large unsorted arrays.
• Average Time Complexity [Big-theta]: Θ(n*log n)
• It is the best Sorting technique used for sorting Linked Lists.