Binary Search

Binary search is a fast search algorithm with run-time complexity of Ο(log n). This search algorithm works on the principle of divide and conquer. For this algorithm to work properly, the data collection should be in the sorted form.

Binary search looks for a particular item by comparing the middle most item of the collection. If a match occurs, then the index of item is returned. If the middle item is greater than the item, then the item is searched in the sub-array to the left of the middle item. Otherwise, the item is searched for in the sub-array to the right of the middle item. This process continues on the sub-array as well until the size of the sub-array reduces to zero.

How Binary Search Works?

For a binary search to work, it is mandatory for the target array to be sorted. We shall learn the process of binary search with a pictorial example. The following is our sorted array and let us assume that we need to search the location of value 31 using binary search.

First, we shall determine half of the array by using this formula −

mid = low + (high - low) / 2

Here it is, 0 + (9 - 0 ) / 2 = 4 (integer value of 4.5). So, 4 is the mid of the array.

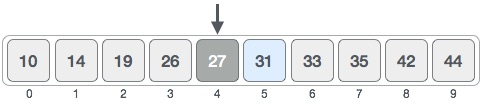
Now we compare the value stored at location 4, with the value being searched, i.e. 31. We find that the value at location 4 is 27, which is not a match. As the value is greater than 27 and we have a sorted array, so we also know that the target value must be in the upper portion of the array.

We change our low to mid + 1 and find the new mid value again.

low = mid + 1
mid = low + (high - low) / 2

Our new mid is 7 now. We compare the value stored at location 7 with our target value 31.

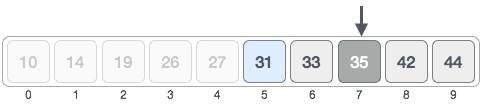
The value stored at location 7 is not a match; rather it is more than what we are looking for. So, the value must be in the lower part from this location.

Hence, we calculate the mid again. This time it is 5.

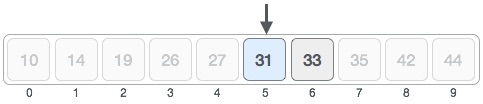
We compare the value stored at location 5 with our target value. We find that it is a match.

We conclude that the target value 31 is stored at location 5.
Binary search halves the searchable items and thus reduces the count of comparisons to be made to very less numbers.

Pseudocode

Procedure binary_search
   A <= sorted array
   n <= size of array
   x <= value to be searched

   Set lowerBound = 1
   Set upperBound = n 

   while x not found
      if upperBound < lowerBound 
         EXIT: x does not exists.
   
      set midPoint = lowerBound + ( upperBound - lowerBound ) / 2
      
      if A[midPoint] < x
         set lowerBound = midPoint + 1
         
      if A[midPoint] > x
         set upperBound = midPoint - 1 

      if A[midPoint] = x 
         EXIT: x found at location midPoint
   end while
   
end procedure

Binary search is a fast search algorithm with run-time complexity of Ο(log n). This search algorithm works on the principle of divide and conquer. For this algorithm to work properly, the data collection should be in the sorted form.

The binary search looks for a particular item by comparing the middle most item of the collection. If a match occurs, then the index of the item is returned. If the middle item is greater than the item, then the item is searched in the sub-array to the left of the middle item. Otherwise, the item is searched for in the sub-array to the right of the middle item. This process continues on the sub-array as well until the size of the subarray reduces to zero.

Binary Search C Program

Code

#include <stdio.h>

#define MAX 20

// array of items on which binary search will be conducted. 
int intArray[MAX] = {1,2,3,4,6,7,9,11,12,14,15,16,17,19,33,34,43,45,55,66};

void printline(int count) {
   int i;
	
   for(i = 0;i < count-1;i++) {
      printf("=");
   }
	
   printf("=\n");
}

int find(int data) {
   int lowerBound = 0;
   int upperBound = MAX -1;
   int midPoint = -1;
   int comparisons = 0;      
   int index = -1;
	
   while(lowerBound <= upperBound) {
      printf("Comparison %d\n" , (comparisons +1) );
      printf("lowerBound : %d, intArray[%d] = %d\n",lowerBound,lowerBound,
         intArray[lowerBound]);
      printf("upperBound : %d, intArray[%d] = %d\n",upperBound,upperBound,
         intArray[upperBound]);
      comparisons++;
		
      // compute the mid point
      // midPoint = (lowerBound + upperBound) / 2;
      midPoint = lowerBound + (upperBound - lowerBound) / 2;	
		
      // data found
      if(intArray[midPoint] == data) {
         index = midPoint;
         break;
      } else {
         // if data is larger 
         if(intArray[midPoint] < data) {
            // data is in upper half
            lowerBound = midPoint + 1;
         }
         // data is smaller 
         else {
            // data is in lower half 
            upperBound = midPoint -1;
         }
      }               
   }
   printf("Total comparisons made: %d" , comparisons);
   return index;
}

void display() {
   int i;
   printf("[");
	
   // navigate through all items 
   for(i = 0;i &;lt; MAX;i++) {
      printf("%d ",intArray[i]);
   }
	
   printf("]\n");
}

void main() {
   printf("Input Array: ");
   display();
   printline(50);
	
   //find location of 1
   int location = find(55);

   // if element was found 
   if(location != -1)
      printf("\nElement found at location: %d" ,(location+1));
   else
      printf("\nElement not found.");
}

Output

Input Array: [1 2 3 4 6 7 9 11 12 14 15 16 17 19 33 34 43 45 55 66 ]
==================================================
Comparison 1
lowerBound : 0, intArray[0] = 1
upperBound : 19, intArray[19] = 66
Comparison 2
lowerBound : 10, intArray[10] = 15
upperBound : 19, intArray[19] = 66
Comparison 3
lowerBound : 15, intArray[15] = 34
upperBound : 19, intArray[19] = 66
Comparison 4
lowerBound : 18, intArray[18] = 55
upperBound : 19, intArray[19] = 66
Total comparisons made: 4
Element found at location: 19

Complexity Analysis of Binary Search

Complexities like O(1) and O(n) are simple to understand. O(1) means it requires constant time to perform operations like to reach an element in constant time as in case of dictionary and O(n) means, it depends on the value of n to perform operations such as searching an element in an array of n elements.
But for O(Log n), it is not that simple. Let us discuss this with the help of Binary Search Algorithm whose complexity is O(log n).

Binary Search: Search a sorted array by repeatedly dividing the search interval in half. Begin with an interval covering the whole array. If the value of the search key is less than the item in the middle of the interval, narrow the interval to the lower half. Otherwise, narrow it to the upper half. Repeatedly check until the value is found or the interval is empty.

Example:

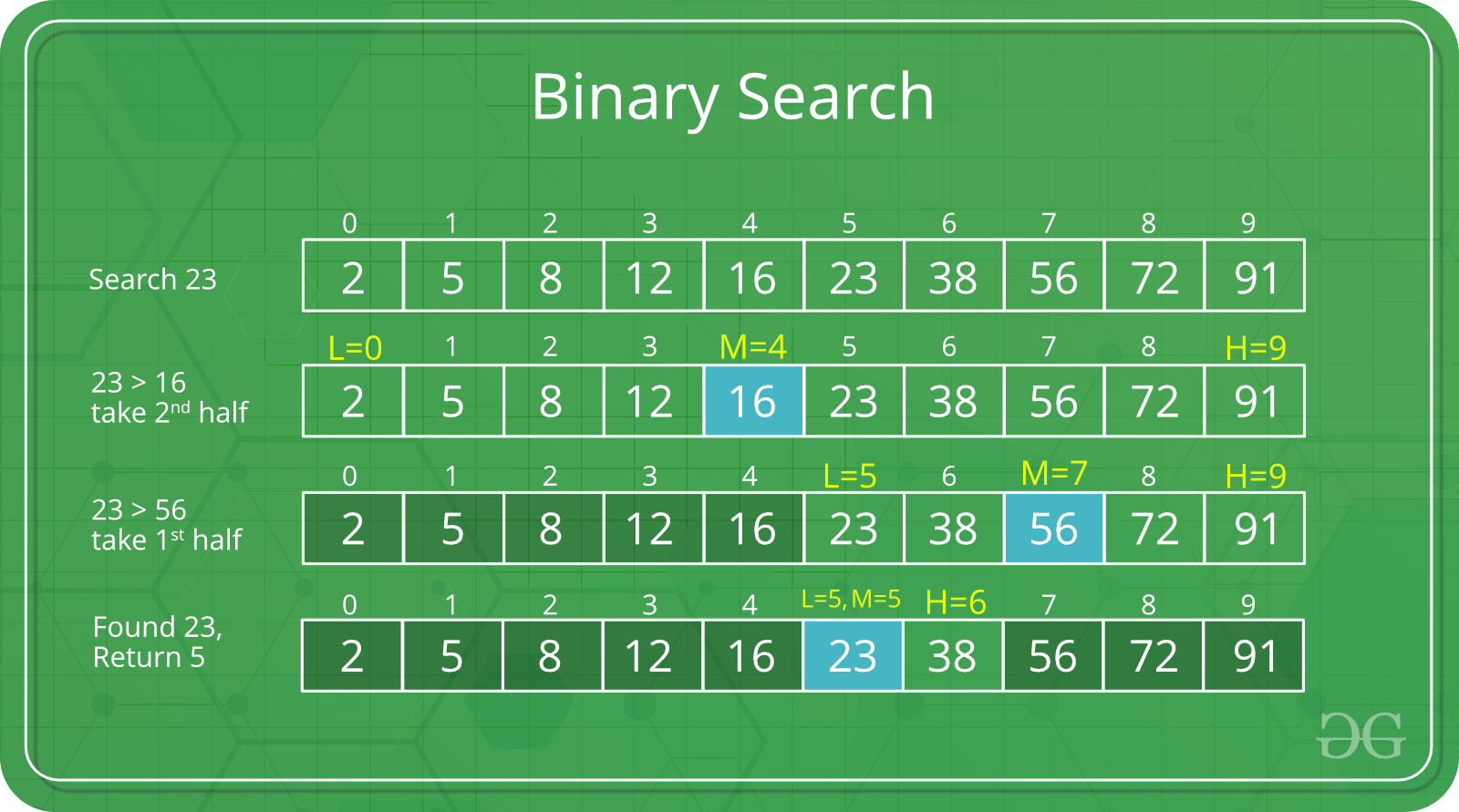
Working Example

Sorted Array of 10 elements: 2, 5, 8, 12, 16, 23, 38, 56, 72, 91

Let us say we want to search for 23.

Finding the given element:

Now to find 23, there will be many iterations with each having steps as mentioned in the figure above:

• Iteration 1:

Array: 2, 5, 8, 12, 16, 23, 38, 56, 72, 91

• Select the middle element. (here 16)
• Since 23 is greater than 16, so we divide the array into two halves and consider the sub-array after element 16.
• Now this subarray with the elements after 16 will be taken into the next iteration.

• Iteration 2:

Array: 23, 38, 56, 72, 91

• Select the middle element. (now 56)
• Since 23 is smaller than 56, so we divide the array into two halves and consider the sub-array before element 56.
• Now this subarray with the elements before 56 will be taken into the next iteration.

• Iteration 3:

Array: 23, 38

• Select the middle element. (now 23)
• Since 23 is the middle element. So the iterations will now stop.

Calculating Time complexity:

• Let say the iteration in Binary Search terminates after k In the above example, it terminates after 3 iterations, so here k = 3
• At each iteration, the array is divided by half. So let’s say the length of the array at any iteration is n
• At Iteration 1,

Length of array = n

• At Iteration 2,

Length of array = ⁿ⁄₂

• At Iteration 3,

Length of array = ⁽ⁿ⁄₂)⁄₂ = ⁿ⁄₂²

• Therefore, after Iteration k,

Length of array = ⁿ⁄₂^k

• Also, we know that after

After k divisions, the length of the array becomes 1

• Therefore

·             Length of array = ⁿ⁄₂^k = 1·            

              => n = 2^k

• Applying log function on both sides:

·             => log₂ (n) = log₂ (2^k)·            

              => log₂ (n) = k log₂ (2)

• Hence, the time complexity of Binary Search is

log₂ (n)

Binary Search Algorithm Advantages

The advantages of binary search algorithm are-

• It eliminates half of the list from further searching by using the result of each comparison.
• It indicates whether the element being searched is before or after the current position in the list.
• This information is used to narrow the search.
• For large lists of data, it works significantly better than linear search.

Binary Search Algorithm Disadvantages

The disadvantages of binary search algorithm are-

• It employs recursive approach which requires more stack space.
• Programming binary search algorithm is error prone and difficult.
• The interaction of binary search with memory hierarchy i.e. caching is poor.(because of its random access nature)