Insertion Sort

Consider you have 10 cards out of a deck of cards in your hand. And they are sorted, or arranged in the ascending order of their numbers. If I give you another card, and ask you to insert the card in just the right position, so that the cards in your hand are still sorted. What will you do?

Well, you will have to go through each card from the starting or the back and find the right position for the new card, comparing its value with each card. Once you find the right position, you will insert the card there.

Similarly, if more new cards are provided to you, you can easily repeat the same process and insert the new cards and keep the cards sorted too.

This is exactly how insertion sort works.

It starts from the index 1(not 0), and each index starting from index 1 is like a new card, that you have to place at the right position in the sorted sub-array on the left.

Following are some of the important characteristics of Insertion Sort:

1. It is efficient for smaller data sets, but very inefficient for larger lists.
2. Insertion Sort is adaptive, that means it reduces its total number of steps if a partially sorted array is provided as input, making it efficient.
3. It is better than Selection Sort and Bubble Sort algorithms.
4. Its space complexity is less. Like bubble Sort, insertion sort also requires a single additional memory space.
5. It is a stable sorting technique, as it does not change the relative order of elements which are equal.

This is an in-place comparison-based sorting algorithm. Here, a sub-list is maintained which is always sorted. For example, the lower part of an array is maintained to be sorted. An element which is to be inserted in this sorted sub-list, has to find its appropriate place and then it has to be inserted there. Hence the name, insertion sort.

How Insertion Sort Works?

Following are the steps involved in insertion sort:

1. We start by making the second element of the given array, i.e. element at index 1, the key. The key element here is the new card that we need to add to our existing sorted set of cards (remember the example with cards above).
2. We compare the key element with the element(s) before it, in this case, element at index 0:
   • If the key element is less than the first element, we insert the key element before the first element.
   • If the key element is greater than the first element, then we insert it after the first element.
3. Then, we make the third element of the array as key and will compare it with elements to it's left and insert it at the right position.
4. And we go on repeating this, until the array is sorted.

Let's consider an array with values {5, 1, 6, 2, 4, 3}

Below, we have a pictorial representation of how insertion sort will sort the given array.

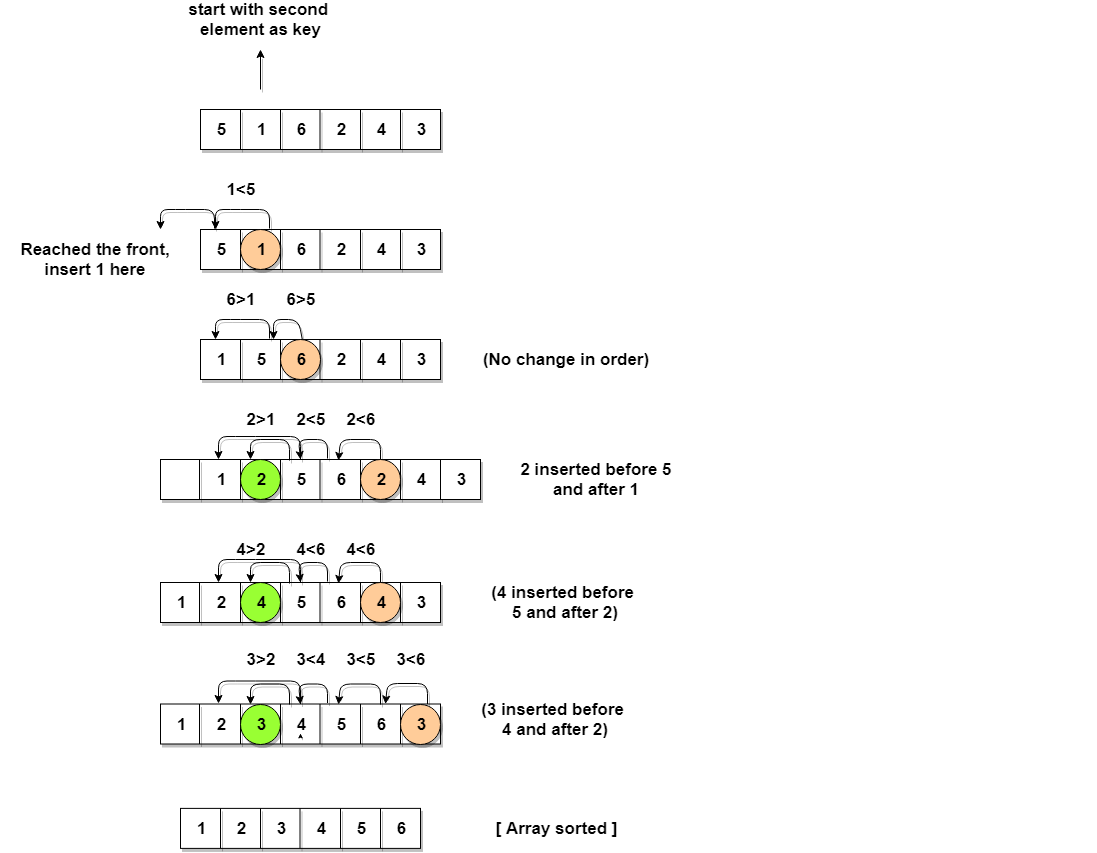
As you can see in the diagram above, after picking a key, we start iterating over the elements to the left of the key. We continue to move towards left if the elements are greater than the key element and stop when we find the element which is less than the key element. And, insert the key element after the element which is less than the key element.

Implementing Insertion Sort Algorithm

Code

#include <stdio.h>
 
void insertionSort(int[],int);
void printArray(int[],int);
 
// main function
int main() 
{
	int array[6] = {5, 1, 6, 2, 4, 3};
	
	printf("Unsorted Array: ");
	// print the unsorted array
	printArray(array, 6);
	
	// calling insertion sort function to sort the array
	insertionSort(array, 6);
	
	printf("\nSorted Array: ");
	// print the sorted array
	printArray(array, 6);
	
	return 0;
}
 
void insertionSort(int arr[], int length) 
{
	int i, j, key;
	for (i = 1; i < length; i++) 
	{
		j = i;
 		while (j > 0 && arr[j - 1] > arr[j]) 
 		{
 			key = arr[j];
 			arr[j] = arr[j - 1];
 			arr[j - 1] = key;
 			j--;
 		}
	}	
}

// function to print the given array 
void printArray(int array[], int size)
{ 
 	int j;
	for (j = 0; j < size; j++)
	{
 		printf("%d ",array[j]);
 	}
}

Output

Unsorted Array: 5 1 6 2 4 3
Sorted Array: 1 2 3 4 5 6

Insertion Sort Algorithm

Now we have a bigger picture of how this sorting technique works, so we can derive simple steps by which we can achieve insertion sort.

1. If it is the first element, it is already sorted. Return 1.
2. Pick next element.
3. Compare with all elements in the sorted sub-list.
4. Shift all the elements in the sorted sub-list that is greater than the value to be sorted.
5. Insert the value.
6. Repeat until list is sorted.

Pseudocode

procedure insertionSort( A : array of items )
   int holePosition
   int valueToInsert
	
   for i = 1 to length(A) inclusive do:
	
      /* select value to be inserted */
      valueToInsert = A[i]
      holePosition = i
      
      /*locate hole position for the element to be inserted */
		
      while holePosition > 0 and A[holePosition-1] > valueToInsert do:
         A[holePosition] = A[holePosition-1]
         holePosition = holePosition -1
      end while
		
      /* insert the number at hole position */
      A[holePosition] = valueToInsert
      
   end for
	
end procedure